2022. 4. 2. 02:23ㆍAlgorithm
이코테 책에서 푼 떡볶이 떡 문제랑 거의 그냥 똑같은 문젠데,,
이상하게 거기서 풀었던대로 (모범답안대로) 풀면 계속 시간초과가 났다...
시간초과 버전:
import sys
input = sys.stdin.readline
n,m = map(int,input().split())
heights = list(map(int,input().split()))
start = 0
end = max(heights)
while start <= end:
total = 0
mid = (start + end) // 2
for i in heights:
if mid < i:
total += i-mid
if m > total:
end = mid - 1
else:
result = mid
start = mid + 1
print(result)
테스트 케이스 다 실행해봐도 답은 나오는데
계속 시간 초과가 났다
결국 다른 분들의 답을 참고해봤는데,
마지막 result에 mid를 받아와서 출력하지 않고,
mid 가 아닌 end를 출력한다는 데에 차이가 있었다.
진짜 저 위의 코드에서 딱 두 줄만 수정하니까 시간 초과가 나지 않았다.
맞았습니다:
import sys
input = sys.stdin.readline
n,m = map(int,input().split())
heights = list(map(int,input().split()))
start = 0
end = max(heights)
while start <= end:
total = 0
mid = (start + end) // 2
for i in heights:
if mid < i:
total += i-mid
if m > total:
end = mid - 1
else:
start = mid + 1
print(end)* else: result = mid 를 삭제했고 print(result)를 print(end)로 수정하였다.
start와 end를 계속 좁혀나가다보면
둘이 만나는 지점 (start = end) 이 생기는데,
둘이 만나게 되면 마지막 반복문이 도는 것이고,
이때 알고리즘상 end = mid-1로 끝나게 되고,
그 값이 '최소한' m이상의 나무를 떼어줄 수 있는 절단기의 최대 높이이기 때문이다.
말로 정리하기는 복잡해 그림으로 표현해봤다:
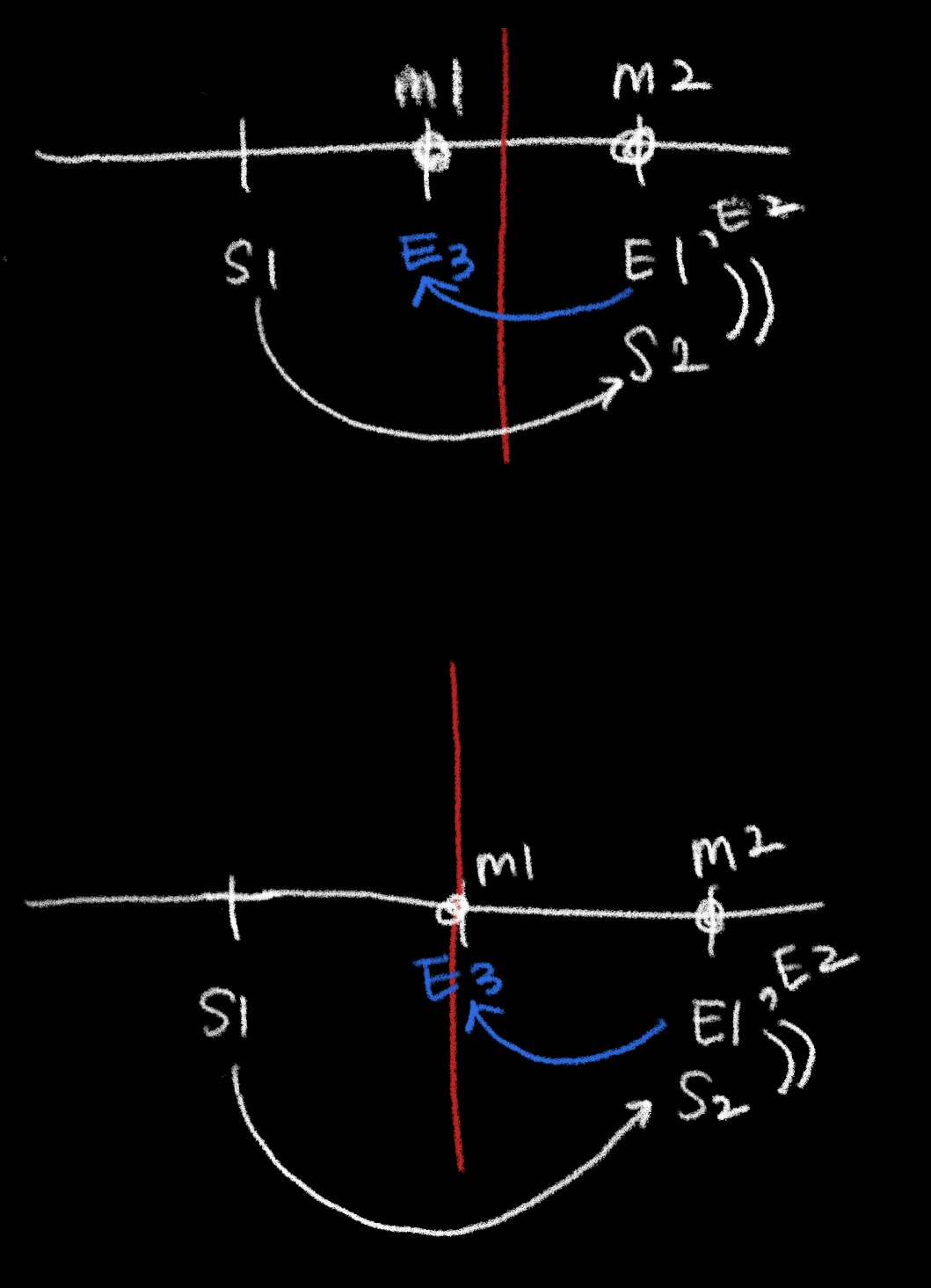
** 정확히 m만큼을 줄 수 있다는 걸 전제로 정리했지만,
사실 정확히 m만큼 주는 것이 불가능한 경우도 있을 것이고, 그럴 경우가 더 많을 것 같다.
아래에서 '적정선'이라 함은 정확히 m만큼은 아니더라도
그에 가장 근접하게 나무를 제공할 수 있는 최선의 값(높이)라고 생각하면 되겠다.
위는 적정선(정확히 m만큼 가져가게 하는 절단기의 높이)이 정수가 아닌 실수인 경우이고,
아래는 정수인 경우이다.
start와 end가 만나는 지점에서는 적정선이 정수든 정수가 아니든 왼쪽편에 있기 때문에 (항상 else 문을 마지막으로 실행),
end = mid -1이 실행되면서 반복문이 끝이 나고,
마지막에 이동시켜준 end 지점이 딱 적정선보다 작은 정수 중에 가장 큰 정수이거나 딱 적정선 값인 거다.
말로는 이해가 힘들다..
그림으로 정리하는 게 최고다.
'Algorithm' 카테고리의 다른 글
| [해시] 프로그래머스 '완주하지 못한 선수' (0) | 2022.04.06 |
|---|---|
| [JAVA] 단순연결리스트의 구현 - 학생부 입력 예제 (5) | 2022.04.05 |
| [BOJ][정렬] 백준 1181번 파이썬 (0) | 2022.03.21 |
| [BOJ][그래프] 백준 7576번 파이썬: 토마토 (0) | 2022.03.19 |
| [BOJ][그래프] 백준 1012번 파이썬: 유기농 배추 (4) | 2022.03.14 |